📦 haribo's box

2.2.9 and 2.2.10 rate equations

5 min read

chem howmuchhowfasthowfar

Reactivity 2.2.9 - rate equations depend on the mechanism of the reaction and can only be determined experimentally
Reactivity 2.2.10 - the order of a reaction with respect to a reactant is the exponent to which the concentration of the reactant is raised in the rate equation.

see 2.2.11 the rate constant, k

  • the order with respect to a reactant can describe the number of particles taking part in the rate-determining step
  • the overall reaction order is the sum of the orders with respect to each reactant

Note

by convention, rate is expressed as a positive value

  • the rate can be evaluated at each time interval by measuring the gradient of the tangent of the curve
  • plotting the rate of reaction against the concentration confirms that the rate of reaction is directly proportional to the concentration of the reactant

this proportional relationship is made into an equation by introducing the rate constant,

in general, for the reaction:

the powers to which the concentrations of reactants are raised to, and , are known as the orders of the reaction.

the overall reaction order is the sum of the individual orders. the rate constant, , has a fixed value for a particular reaction at a specified temperature.

Warning

the orders of the reaction can only be determined experimentally

the rate equation and reaction mechanism
  • the rate of reaction depends on the rate-determining step
  • the rate equation for the overall equation depends on the rate equation for the rate-determining step
  • since the rate-determining step is an elementary step, its rate equation comes directly from its molecularity

2.2.2 collision theory says that the concentration of each reactant in the rate-determining step must appear in the rate equation for that step, raised to the power of its coefficient in the equation.

equation for rate-determining stepmolecularityrate equation
unimolecular
bimolecular
bimolecular

Warning

these relationships exist only for elementary steps and not for deriving the rate equation for the overall reaction from the stoichiometric coefficients

  • the rate equation for the rate-determining step leads to the rate equation for the overall reaction

  • if the rate-determining step is the first or only step in the mechanism, then its rate equation is the same as the rate equation for the overall reaction

  • when the rate-determining step is not the first step in the mechanism, its reactant concentrations will depend on an earlier step, so that must be taken into account as well

for the reaction:

the following reaction mechanism has been proposed

the rate equation depends on step 2 for which the rate equation is

since is an intermediate, so it cannot appear in the rate equation. because it is a product of step 1, the concentration of the intermediate depends on

so, the rate equation for the overall reaction is

Warning

mechanisms are described as possible mechanisms because they fit the empirical findings - both the kinetic data and overall stoichiometry of the reaction.

at most, mechanisms can be stated to be consistent with data, they cannot be proven to be correct

graphical representations

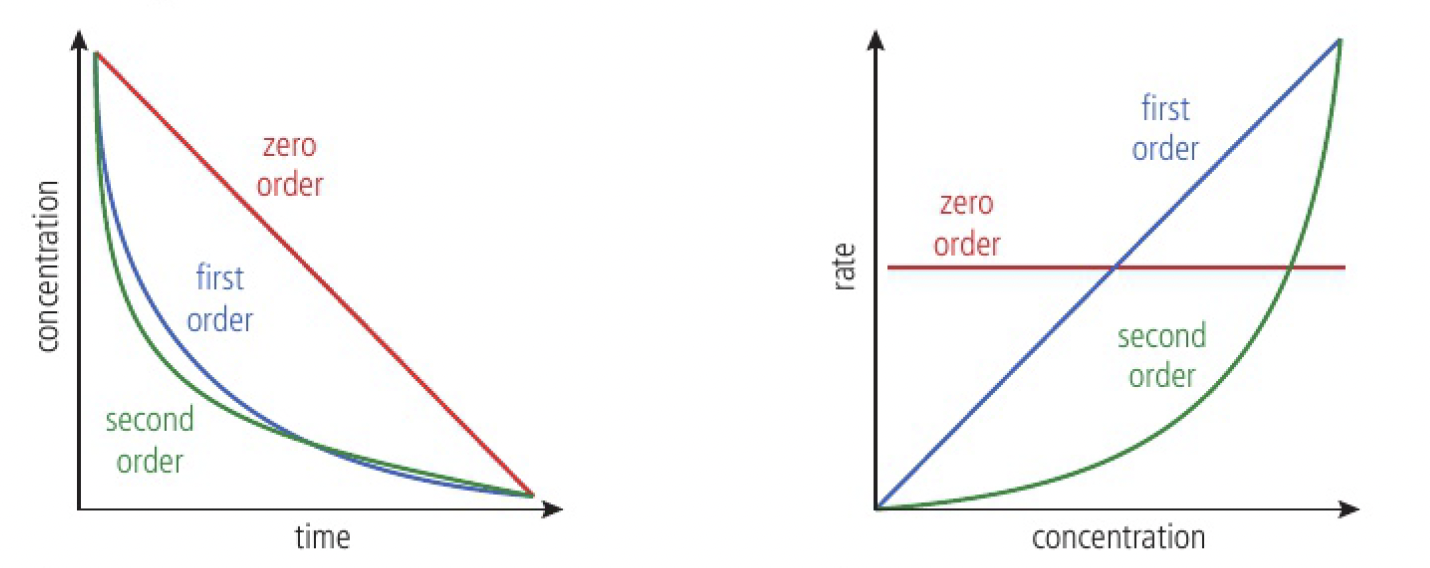
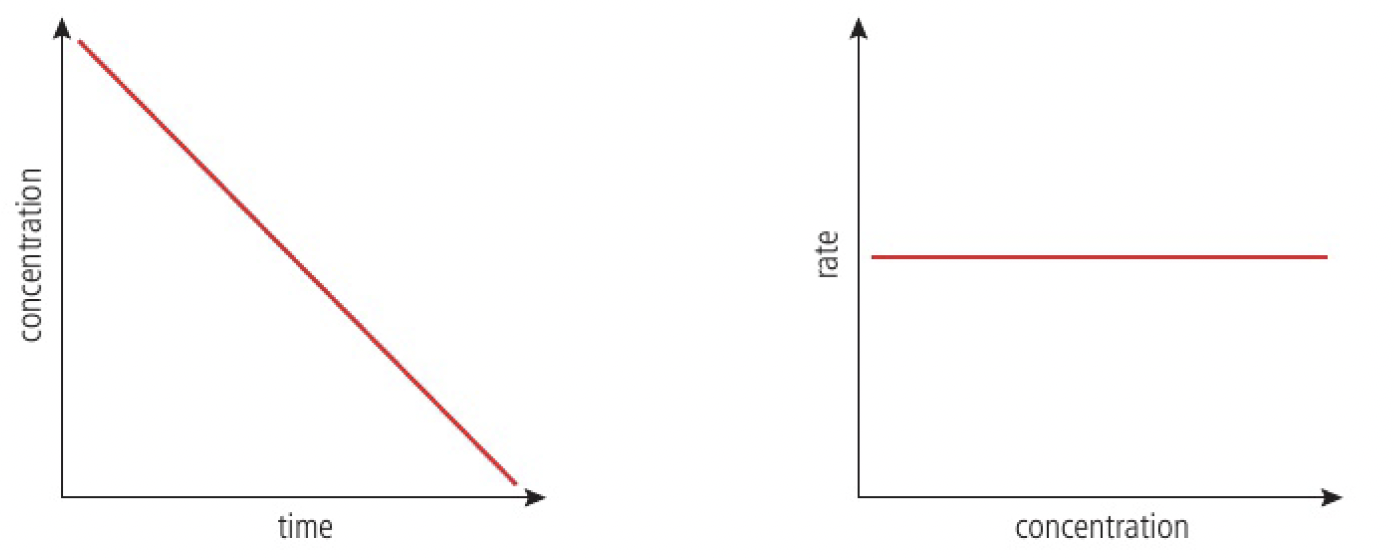
the order with respect to a particular reactant () can be fractional and negative values, but only zero, first, second order reactions need to be known here.

zero-order reaction

the rate is not affected by the concentration of

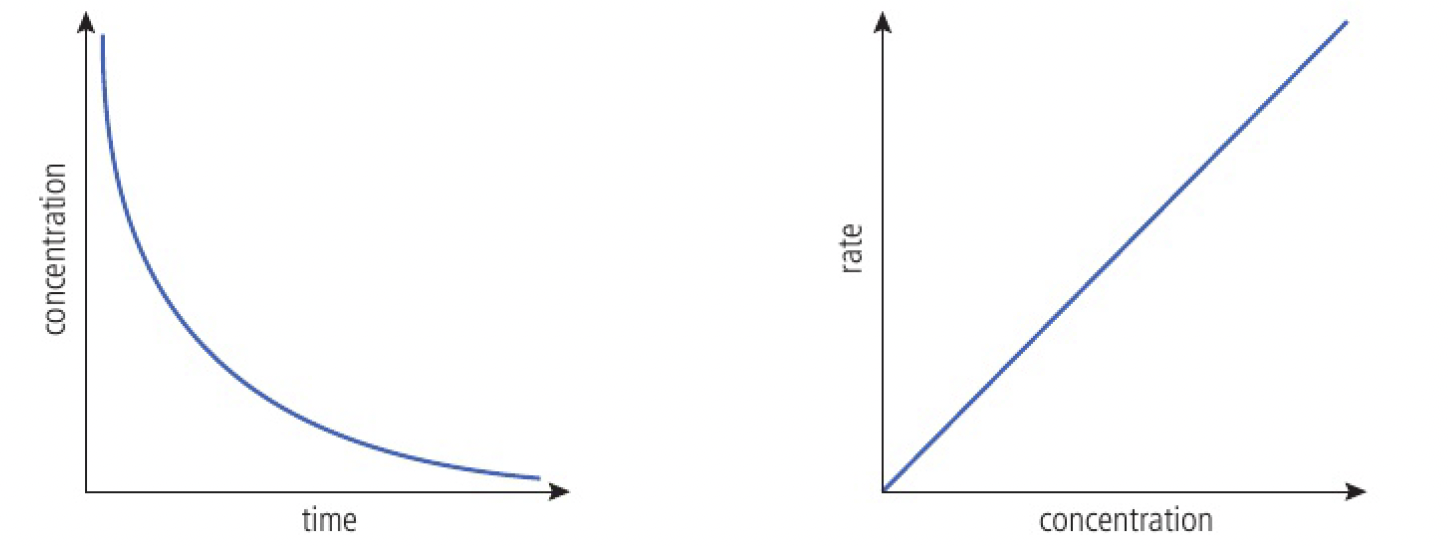
first-order reaction

the rate is directly proportional to the concentration of

second-order reaction

the rate is proportional to the square of the concentration of

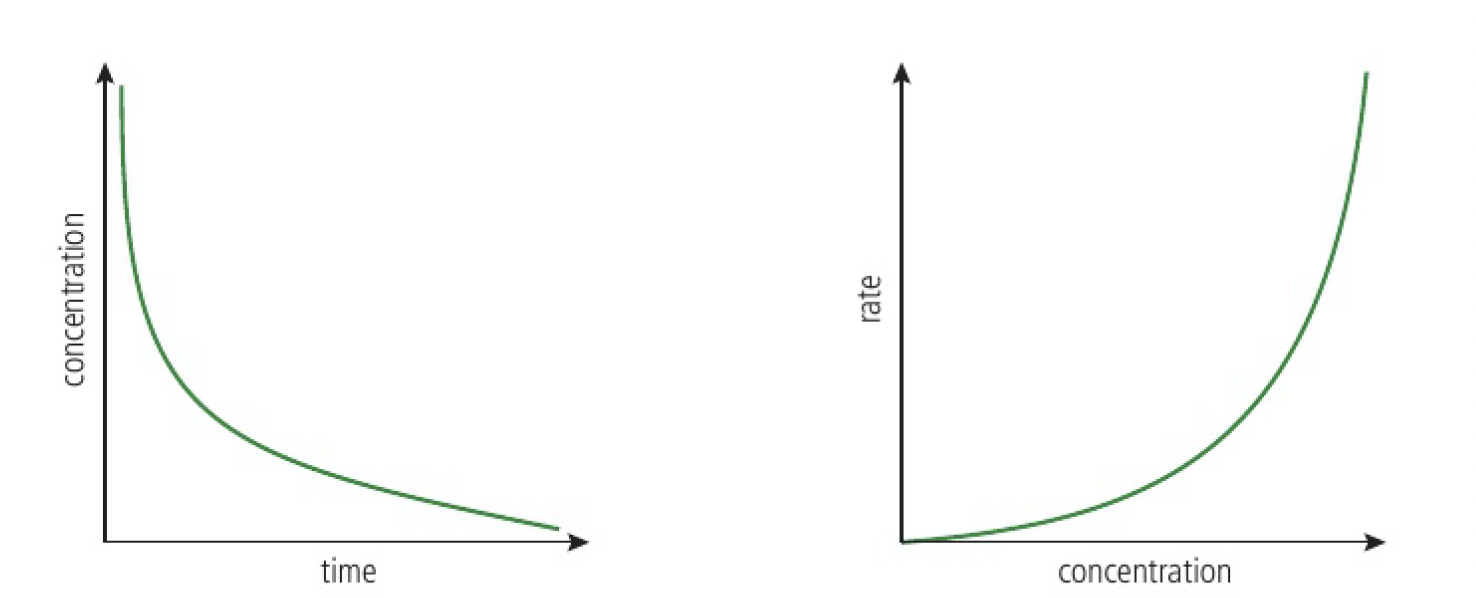
  • the concentration-time graph is steeper at the start and levels off more quickly
  • the rate-concentration graph is a parabola
determination of the overall order of a reaction
  • methods depend on determining the order with respect to each reactant in turn
  • there are two main methods, but only the initial rates method is covered at this level
    • it is discussed with respect to two reactants, and .
initial rates method
  • this involves carrying out several separate experiments with different starting concentrations of reactant , and measuring the initial rate of each reaction. the concentrations of other reactants are held constant
  • the process can then be repeated for reactant B

by analysing the data, the order of reaction can be deduced

  • if changing the concentration of has no effect on the rate, the reaction must be zero order with respect to A
  • if changing the concentration of produces directly proportional changes in the rate of reaction, the reaction must be first order
  • if changing the concentration of produces the square of that change, then the reaction must be second-order
    • ie doubling concentration leading to a 4 times increase in the rate of equation
change in rate of zero-order reactionchange in rate of first-order reactionchange in rate of second-order reaction
doublesno change
triplesno change
quadruplesno change
using the integrated form of the rate equation
  • not needed for the IB diploma
  • taking the integrated form of the rate equation allows for direct graphical analysis of functions of concentration of time.
challenge questions
  1. radioactive decay is always a first-order process. therefore, if we measure the time it takes for the concentration of a radioisotope to decrease to half its value, we find that this interval is independent of the starting concentration. this value, known as the half-life, , for the reactant, is therefore a constant.

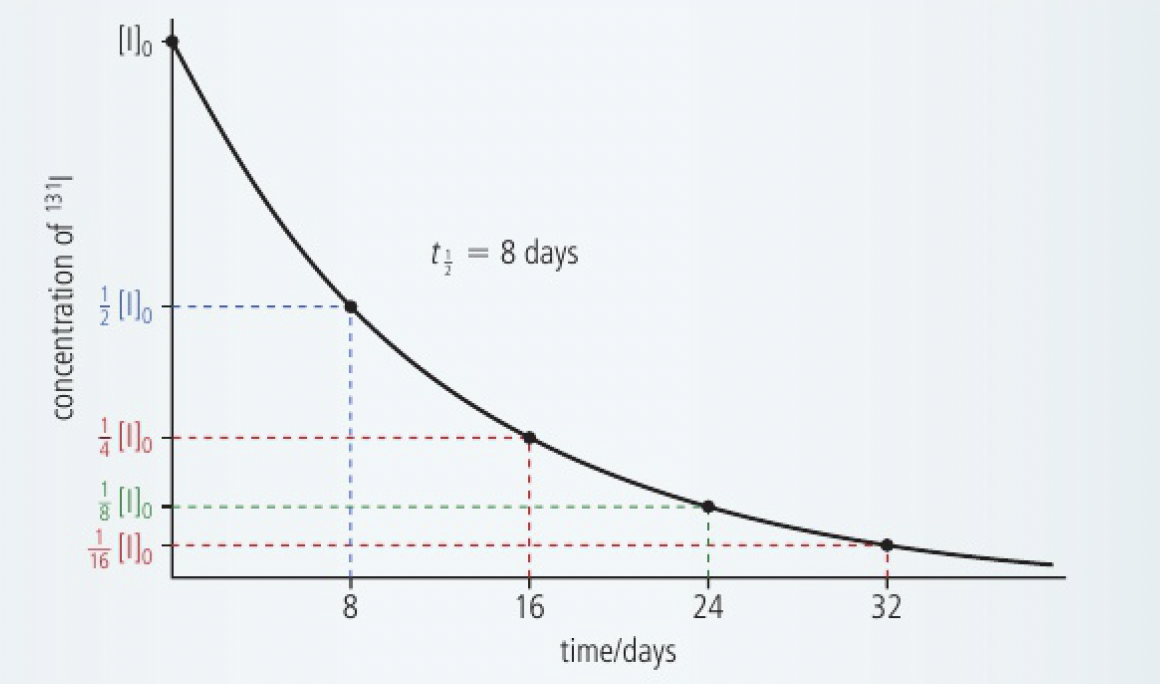
    given that for is 8 days, calculate the mass of remaining after 24 days in a sample initially containing .

Backlinks