Reactivity 2.2.12 - the Arrhenius equation uses the temperature dependence of the rate constant to determine the activation energy
Reactivity 2.2.13 - the Arrhenius factor,
the Arrhenius equation is used to determine the activation energy of a reaction
the rate of reaction depends on two things:
- the rate constant,
- the concentrations of reactants raised to a power
since increasing temperature doesn’t change the concentration, its effect must be on the value of
collision theory explains the effect of increasing temperature:
- more collisions that involve particles having the activation energy
- a greater proportion of collisions leading to reaction
Maxwell-Boltzmann energy distribution curves can be used to show the changing distribution of kinetic energies with increasing temperature
- when the activation energy is large, a temperature rise will cause a significant increase in the number of particles
- when the activation energy is small, a temperature rise will cause a smaller effect on the reaction rate
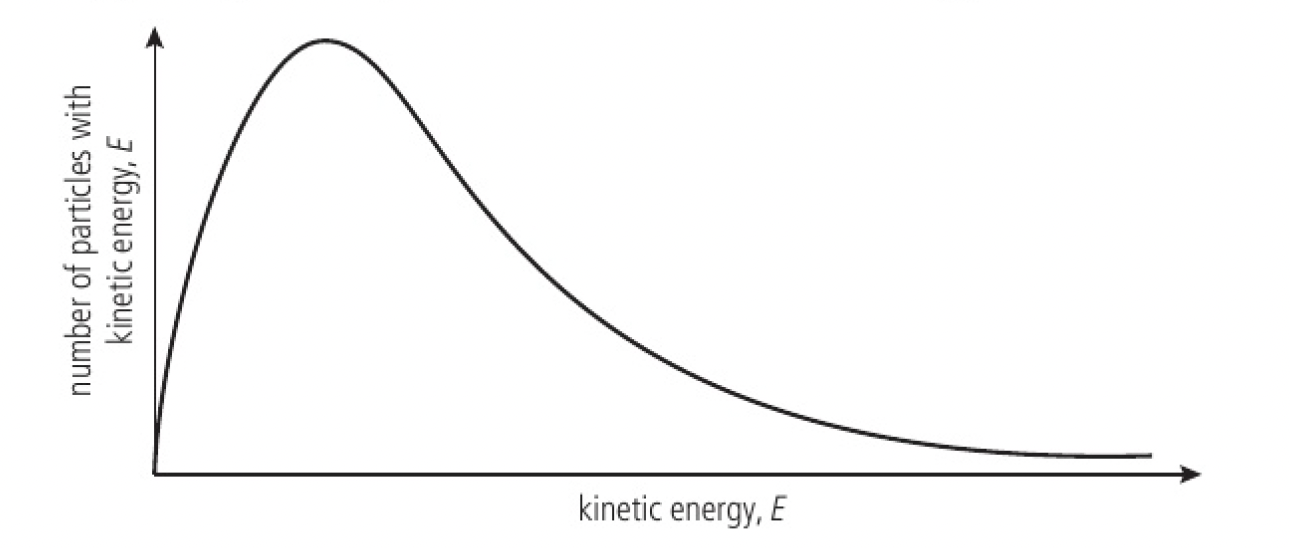
the temperature dependence of rate constant is expressed in the Arrhenius equation
Svante Arrhenius showed that the fraction of molecules with energy greater than the activation energy is proportional to
this can be written as
where
takes into account the frequency with which successful collisions will occur based on collision geometry - constant for a reaction
- has the same units as
(and varies depending on the order of the reaction)
calculation with the Arrhenius equation
the equation of a straight line
taking the natural logarithm of the Arrhenius equation:
this is in the form of
the Arrhenius plot is the graph of
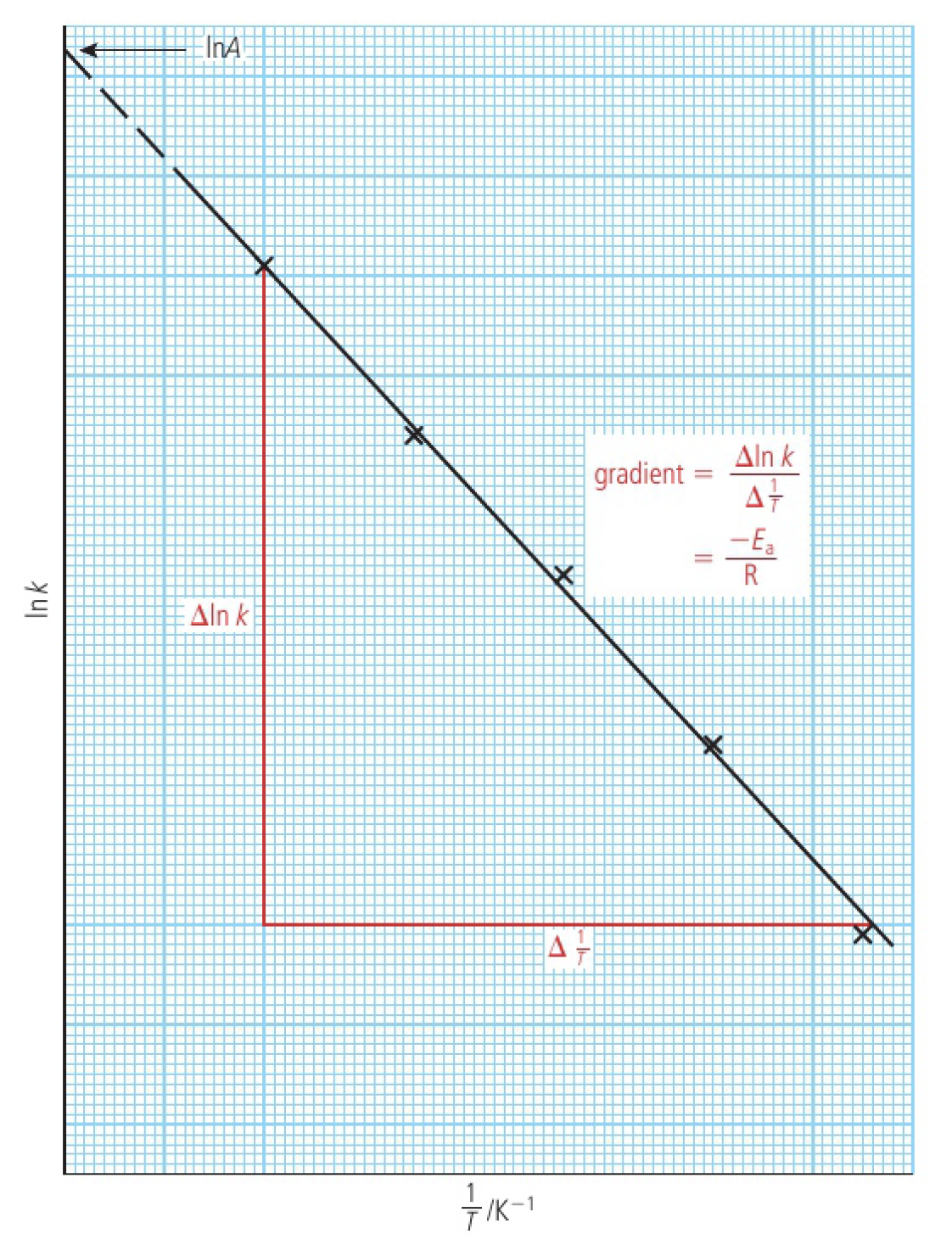
solving simultaneous equations
activation energy can also be calculated from values of
at temperature
at temperature
subtracting the second from the first:
(equation given in data booklet)