chem whatdriveschemicalreactions
Reactivity 1.2.5 - a Born-Haber cycle is an application of Hess’s law, used to show energy changes in the formation of an ionic compound
see 1.2.2 Hess’s law
first ionisation energies and electron affinities
the first ionisation energy corresponds to the energy needed to form the positive ion from a gaseous atom:
this process is endothermic as it involves pulling an electron away from the attractive electrostatic force due to the positively charged nucleus.
the electron affinity is the enthalpy change when one mole of gaseous atoms attracts one moles of electrons:
as the electron is attracted to the positively charged nucleus, the process is exothermic
lattice enthalpies
adding the two equations for ionisation energy and electron affinity:
it can be seen that the electron transfer process is endothermic overall, so energetically unfavourable despite forming ions with stable noble gas electron configurations.
the oppositely charged gaseous ions come together to form an ionic lattice, which is a very exothermic process as there is a strong attraction between the oppositely charged ions
it is this step that explains the readiness of sodium and chlorine to form an ionic compound
the lattice enthalpy expresses the enthalpy change in terms of the revers endothermic process - ie the solid lattice breaking into gaseous ions
experimental lattice enthalpies and the Born-Haber cycle
the Born-Haber cycle is used to determine lattice energies. for example, the formation of sodium chloride:
this can be considered to take place in several steps
- sodium is atomised
the corresponding enthalpy change is known as the enthalpy change of atomisation
- one mole of chlorine atoms is formed as ½ mole of
bonds break
- one electron is removed from the outer shell of the gaseous sodium atom
- one electron is added to the outer energy level of the gaseous chlorine atom
- the gaseous ions come together to form one mole of solid sodium chloride
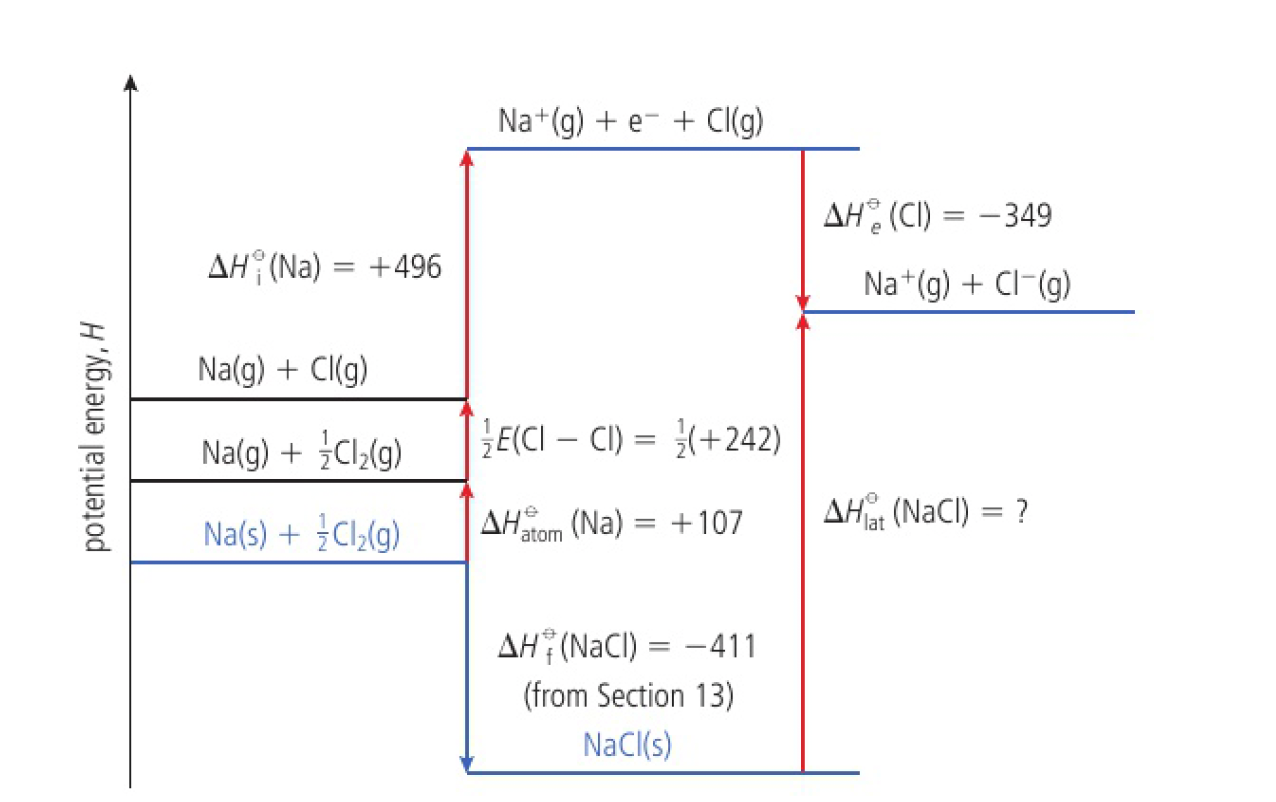
this allows an equation for the lattice enthalpy to be expressed in terms of experimentally verifiable quantities: