chem modelsofparticulatenatureofmatter
Structure 1.5.3 - the molar volume of an ideal gas is constant at a specific temperature and pressure
Structure 1.5.4 - the relationship between the pressure, volume, temperature and amount of an ideal gas is shown in the ideal gas equation
proportionality/inverse proportionality can be figured out by looking at
molar volume
according to avogadro’s law, the volume occupied by one mole of any gas is the same since the particles in a gas have negligible volume compared with the volume the gas occupies.
number of moles of gas (
ideal gas equation
the gas equation and avogadro’s law can be combined to give
this can be made into an equation by introducing a constant,
real gases
an ideal gas is defined as one that obeys the ideal gas law under all conditions. this means that for one mole of gas,
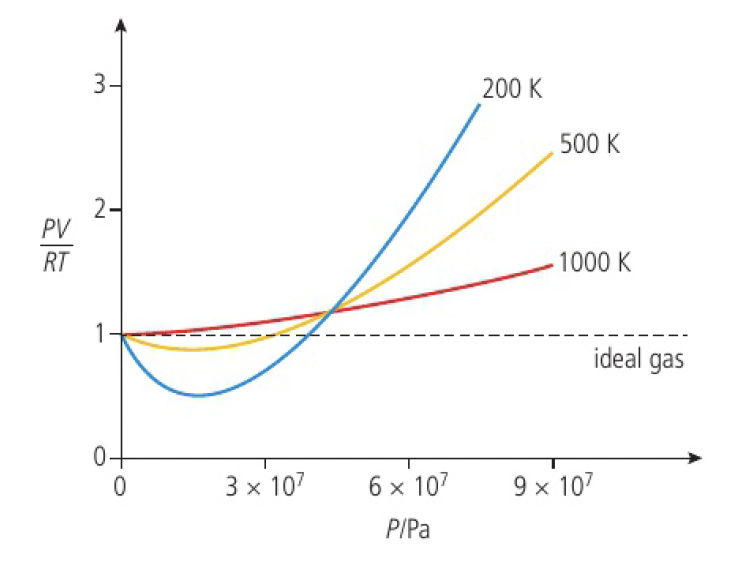
this graph lets us draw some conclusions, that:
- gases behave most like an ideal gas at low pressure and shows the greatest deviation at high pressure
- gases behave most like an ideal gas at high temperature and shows the greatest deviation at low temperature
- if the volume of the gas particles is not negligible,
- there are attractive forces between the particles,
van der Waal’s equation takes into account the measure of attraction between the particles (a) and the volume excluded by the particles (b)
challenge questions
- Consider a sample of gas at pressure
, volume , and temperature (K) which is expanded to a new volume at constant temperature with a new pressure
a) state the relationship between, , and for expansion at constant temperature
b) the gas is then heated at constant volume
c) deduce a relationship between the initial conditions and the final conditions.
derive combined gas equation from substitution in a)
- Blowing up a balloon increases its volume as the number of particles increases. What do you think would happen to this inflated balloon at the top of a very high mountain?
at the top of a very high mountain, the pressure would be lesser than that of lower altitudes, so the volume would increase.
- a) calculate the volume of
of steam at a temperature of and a pressure of and show that the volume occupied by the particles is negligible.
consider the volume that 18g of water in its liquid form occupies, 18cm
% volume occupied by water molecules =
b) show that the volume occupied by the particles is not negligible when the pressure is increased to
% volume occupied by water molecules =
- show that the van der Waal’s equation correctly predicts values of
for 1 mol of gas at very high pressures
at high pressures,
hence,
- show that the van der Waal’s equation correctly predicts values of
for 1 mol of gas at very low pressures
at low pressures,
hence,