1.3.3, 1.3.4, and 1.3.5 electron configuration

chem modelsofparticulatenatureofmatter

Structure 1.3.3 - The main energy level is given an integer number, , and can hold a maximum of electrons.

Structure 1.3.4 - A more detailed model of the atom describes the division of the main energy level into s, p, d, and f sublevels of successively higher energies

Structure 1.3.5 - Each orbital has a defined energy state for a given electron configuration and chemical environment, and can hold two electrons of opposite spin.

Sub levels contain a fixed number of orbitals, regions of space where there is a high probability of finding an electron

reading

light could be described by frequency (a wave property) or by the energy of individual particles, (photons, or quanta, of light)

these two properties are related by the Planck equation

neither model (of light as a particle or a wave) gives a complete explanation of its properties, so both are needed

• diffraction of light when light passes through a small slit can only be explained by the wave model
• the scattering of electrons that occurs when light is incident on a metal surface is best explained using a particle model of light

similarly, it is more preferable to think of an electron as having wave properties, i.e. the diffraction pattern produced when a beam of electrons is passed through a thin sheet of graphite.

limitations of the Bohr atomic model:

• failed to predict spectral lines of atoms with more than one electron
• assumes that the electron’s trajectory can be precisely described
  • measuring the position of an electron will disturb its motion

n and l are sometimes known as quantum numbers, where n represents the main energy level and l represents the sublevel

Schrödinger model of the hydrogen atom

• proposed that a wave equation could be used to describe the behaviour of an electron in the same way a wave equation could be used to describe the behaviour of light
• this equation can be applied to multi-electron systems
• the solutions are known as atomic orbitals
  • a region around a nucleus in which there is a 90% probability of finding the electron
  • the shape of the orbitals depend on the energy of the electron
  • higher energy higher probability of being found further from the nucleus
    limitations:
• does not account for electron spin
  • electrons can also be thought to spin on their own axis as well as moving around the nucleus
  • they can spin clockwise, represented by and anticlockwise, represented by

shape of atomic orbitals

the s orbital is shaped like a sphere
the p orbital is shaped like a “dumbbell”

• the difference is in their orientation in space
• think of it as a cube with the nucleus at the centre … if that makes sense

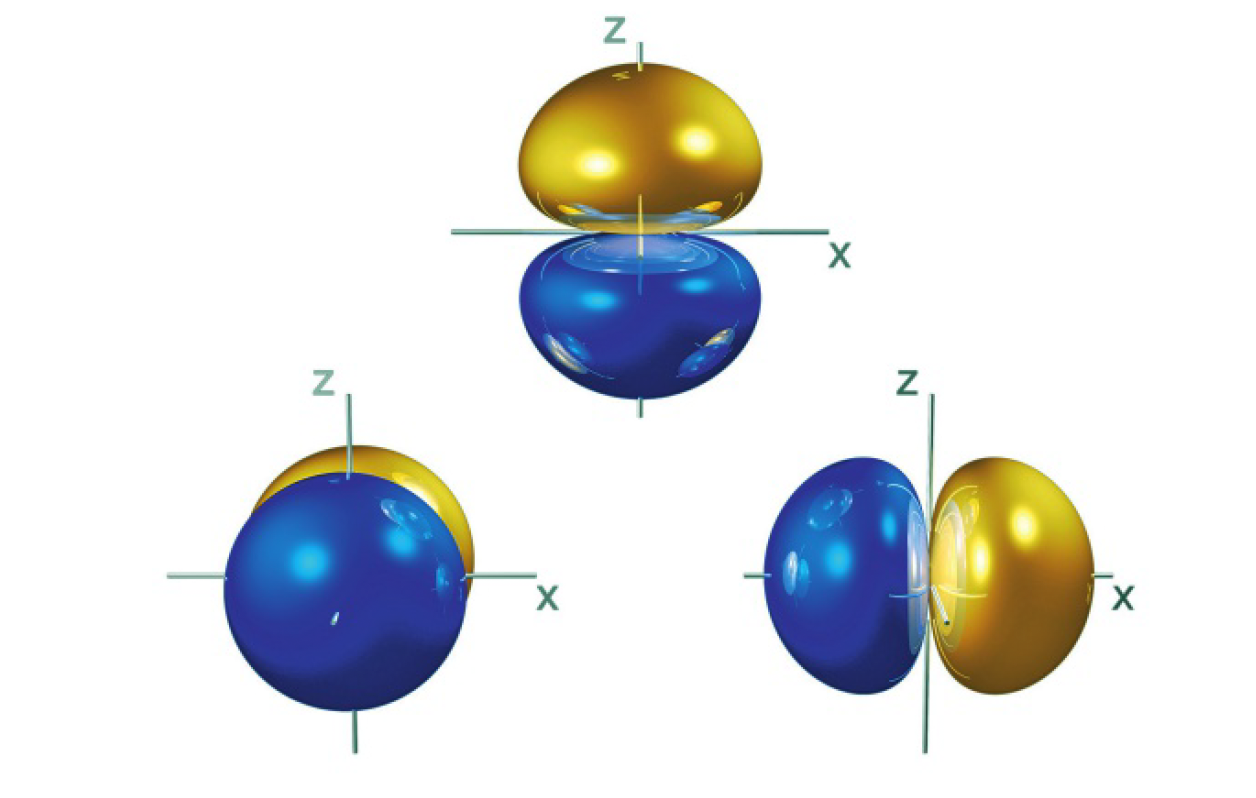
the first energy has one 1s orbital:

• max of 2 electrons
• to highlight the distinction between this wave description of the electron provided by the Schrödinger model and the circular orbits of the Bohr model, it can be said that the electron occupies a 1s orbital

the second energy level has a 2s and 2p sublevel:

• this energy level is split into 2 sublevels - 2s and 2p
• 2s has one 2s orbital, 2p has three 2p orbitals so max 6 electrons for 2p sublevel
• the three 2p atomic orbitals have equal energy, degenerate

d and f orbitals

• the th energy level of the atom is divided into sublevels
• the third energy level is made up of three sublevels: 3s, 3p, and 3d
• the d sublevels are made up of 5 d orbitals

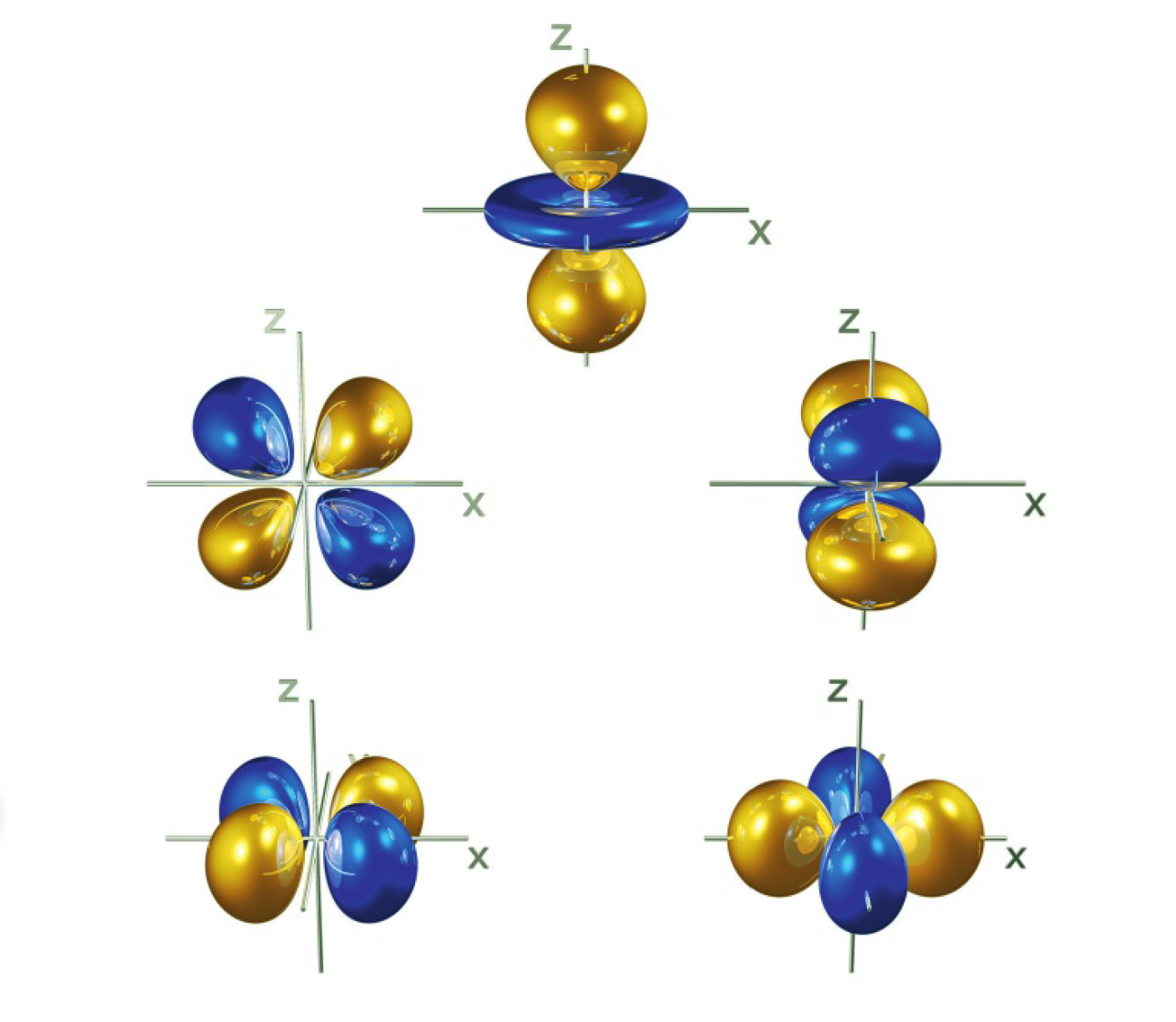(don’t need to know what these shapes are called, only s and p needed)

• the 4f sublevels are made up of seven f atomic orbitals

electron configuration

Each main energy level of electrons is divided into sublevels

ˆsimplification

degenerate orbitals of the same energy form a sublevel:

• 1 s orbital forms an s sublevel
• 3 p orbitals form a p sublevel
• 5 d orbitals form a d sublevel
• 7 f orbitals form an f sublevel

Heisenberg’s Uncertainty Principle:

• we cannot know where an electron is at any given moment in time
• a probability picture of where the electron is likely to be is the best that can be achieved

Pauli exclusion principle:

• an orbital can hold only two electrons of opposite spin

the electron can be considered to have wave properties and only a probability description of its location is possible at a given time

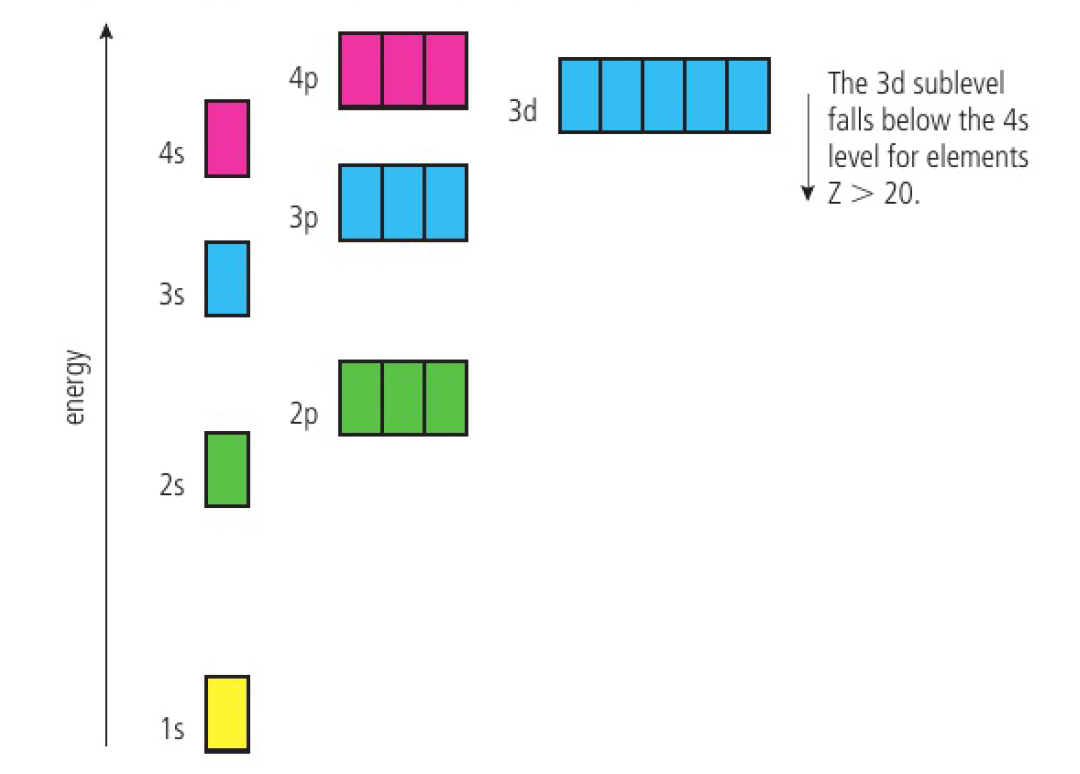
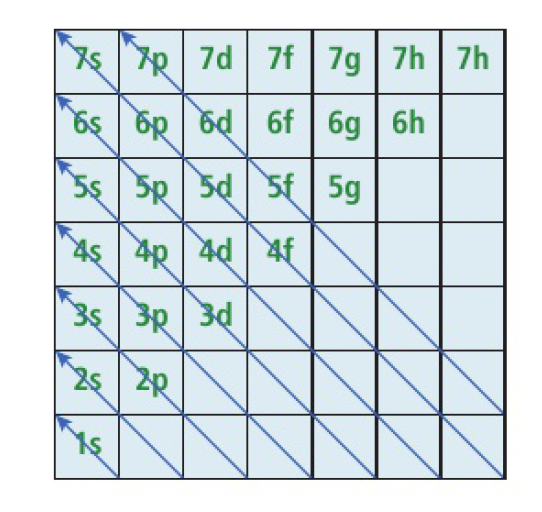
Aufbau principle:

• electrons are placed into orbitals of lowest energy first
• i.e. 1s then 2s then 2p then 3s then 3p then 4s then 3d etc
  

Hund’s rule:

• every orbital in a sublevel is singly occupied with one electron before any one orbital is doubly occupied, and all electrons in singly occupied orbitals have the same spin
• half-filled and fully filled sublevels are particularly stable
• this minimises the mutual repulsion

!!! write 3d before 4s for d block elements !!!

• the energy of an orbital depends on the attraction between the electrons and the nucleus and inter-electron repulsions
• the relative energy of the orbitals change with nuclear charge and the atomic numbers
• the 3d and 4s levels are very close. electrons are first lost from the 4s sublevel
  • when transition metals form their ions, as once the 3d sublevel is occupied, the 3d electrons push the 4s electrons to higher energy

vanadium electron configuration:

• the 3d sub-shell is written before the 4s since the 3d sublevel falls below the 4s orbital once the 4s orbital is occupied

• electron configurations can also be written in condensed/abbreviated form, where the inner electrons are represented as a noble gas core

thus, vanadium can be written as

the electrons in the outer energy level are called valence electrons and are mainly responsible for compound formation

electron configuration of ions

• positive ions are formed by the loss of electrons - from the outer sublevels

e.g. aluminium

when cations are formed for transition metals, the outer 4s electrons are removed before the 3d electrons

for example, chromium:

for example, iron:

the electron configurations of negative ions are determined by adding the electrons into the next available electron orbital:

for example, sulfur:

electron configuration and the periodic table

• elements whose valence electrons occupy an s sublevel make up the s block
• elements whose valence electrons occupy an p sublevel make up the p block
• elements whose valence electrons occupy an d sublevel make up the d block
• elements whose valence electrons occupy an f sublevel make up the f block

exceptions

• chromium and copper and table below
• using Hund’s rule - half-filled and filled sublevels seem to be particularly stable

chromium:

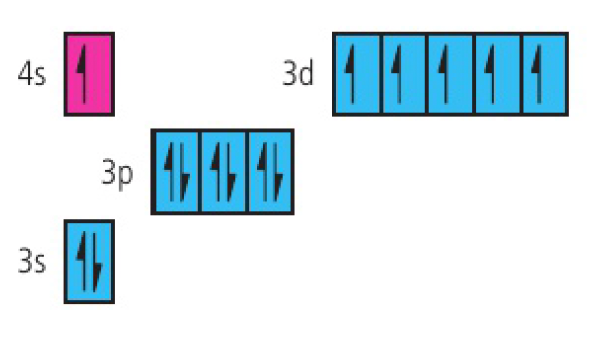
copper:

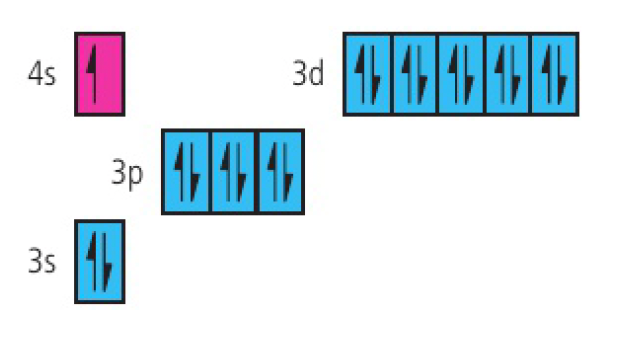
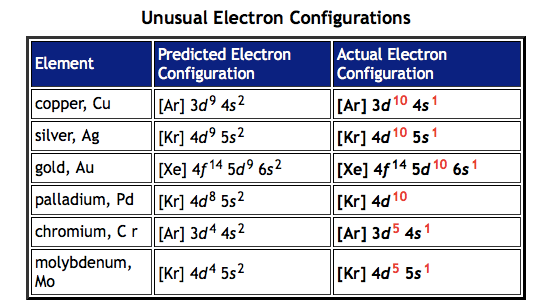
challenge questions

2. State two ways in which the Schrödinger model of the hydrogen atom differs from that of the Bohr model.

one: it does not prescribe a fixed orbit for the electron
two: it does not treat the electron as a localised particle, but gives a probability wave description

3. What provides evidence to support the Bohr model of the hydrogen atom?

The energy of the lines in the emission spectra of atomic hydrogen.

4. State the electron configuration of thorium.

5. Only a few atoms of element 109. meitnerium, have ever been made. Isolation of an observable quantity of the element has never been achieved and may well never be. This is because meitnerium decays very rapidly.
   a) suggest the electron configuration of the ground-state atom of the element.

   b) there is no g block in the periodic table as no elements with outer electrons in g orbitals exist in nature or have been made artificially. Suggest a minimum atomic number for such an element.

   is 118 and has a full p sublevel, so would be 3 extra electrons.

6. Consider how the shape of the periodic table is related to the three-dimensional world we live in.
   a) How many 3p and 3d orbitals would there be if only the x and y dimensions existed?

   there would be 2 3p orbitals and 2 3d orbitals

   b) How many groups in the p and d block would there be in such a two-dimensional world?

   there would be 4 and 4